lc难点精选：备战麦克罗索夫特

3 minute read

二叉树与链表

二叉树和链表题一直是我的难点：

展开为链表比较简单，只需要左右子树递归：

114（展开为先序遍历）剑指offer36（展开为中序遍历）

链表转为二叉树比较难的。

例：109

给定一个单链表，其中的元素按升序排序，将其转换为高度平衡的二叉搜索树。本题中，一个高度平衡二叉树是指一个二叉树每个节点的左右两个子树的高度差的绝对值不超过 1。

这个技巧是每次都找最中间那个节点作为根。链表找中点就得用快慢指针了。

找完中点之后就递归。这里可以把mid节点前面的edge切掉，后面的edge也切掉，再分别在左右两个头上递归。like this.

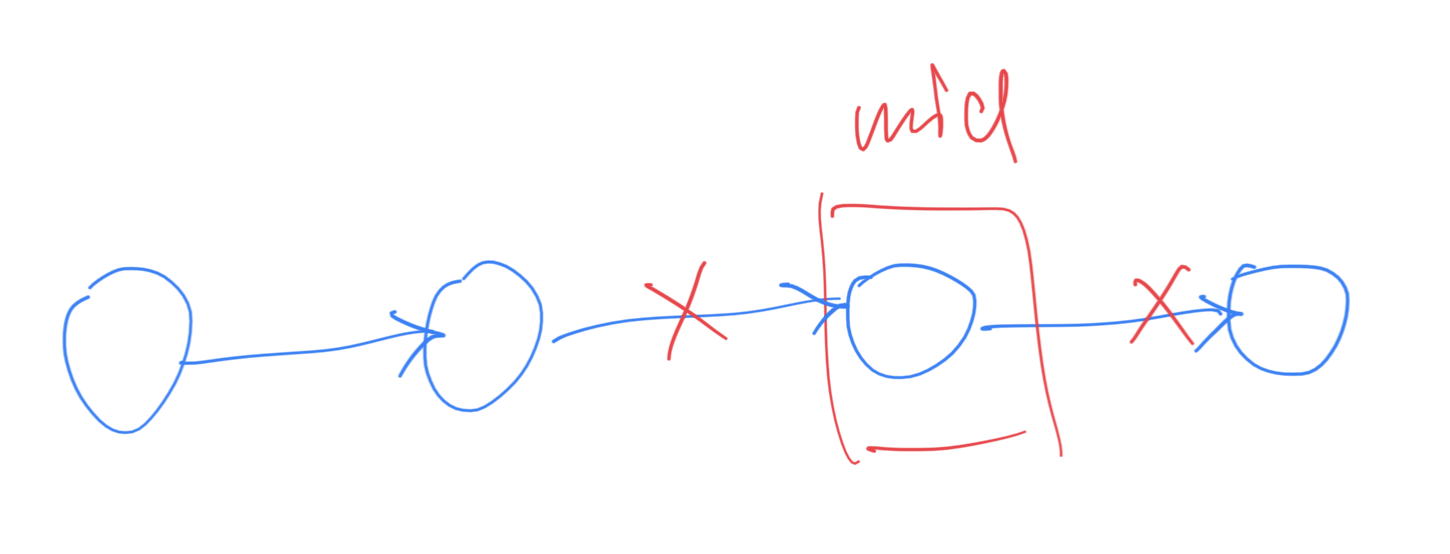
binary1

切后面好做，mid->next保存下来然后让mid->next = nullptr.

切前面的话得从头再遍历到mid之前的那个节点。我封装了一个cutBefore()函数。

至于正确性证明，只要证明“节点数最多相差1的两个子树，其高度最多相差1”就可以了。

BST删除

过于经典，从61b开始已经写了n遍了还是反应不过来。爷佛了。

每次都走到死胡同，错误解法：

假设找到左子树最大节点。findMax(u->left)，然后把自己的值替换为该节点的值。再递归地从左子树中删掉那个节点。这个方法的问题是：无法定位toDelete节点的父亲。如果toDelete节点是叶子的话就很jb麻烦。太烦了！

正确解法：利用递归返回值

给我记住。

class Solution {
public:
    TreeNode* deleteNode(TreeNode* root, int key) 
    {
        if (root == nullptr)    return nullptr;
        if (key > root->val)    root->right = deleteNode(root->right, key);     // 去右子树删除
        else if (key < root->val)    root->left = deleteNode(root->left, key);  // 去左子树删除
        else    // 当前节点就是要删除的节点
        {
            if (! root->left)   return root->right; // 情况1，欲删除节点无左子
            if (! root->right)  return root->left;  // 情况2，欲删除节点无右子
            TreeNode* node = root->left;           // 情况3，欲删除节点左右子都有 
            while (node->right)          // 寻找欲删除节点左子树的最右节点
                node = node->right;
            node->right = root->right;    // 将欲删除节点的右子树成为其左子树的最右节点的右子树
            root = root->left;         // 欲删除节点的左子顶替其位置，节点被删除
        }
        return root;    
    }
};

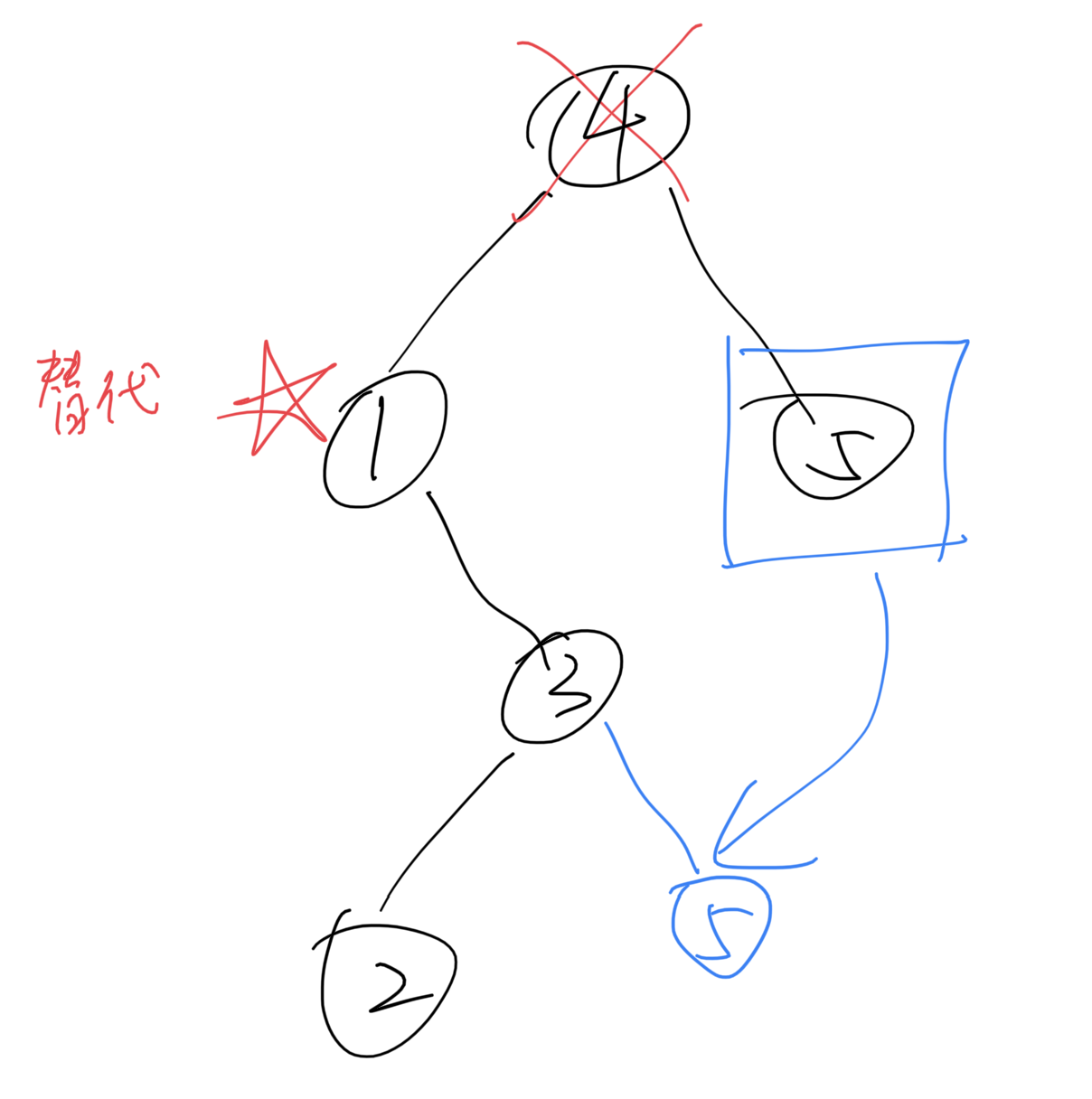
这里很妙的地方是直接把“待删除节点的右子树变成（欲删除节点左子树的最右节点的）右子树”。可以看到结果是完全合法的。

所以不要想着把“3”直接移到“4”的位置。虽然也是合法的，但麻烦很多。

下一个更大元素

31.下一个排列 & 556.下一个更大元素III，基本是一样的。

基本思路：

从右向左走，碰到第一个下降元素停止，下标记为i。如果碰不到下降元素，说明已经是最大排列。
在i的右边找到大于i的最小数。下标记为j。（肯定能找到）
swap(a[i], a[j])
reverse i右边的所有元素。

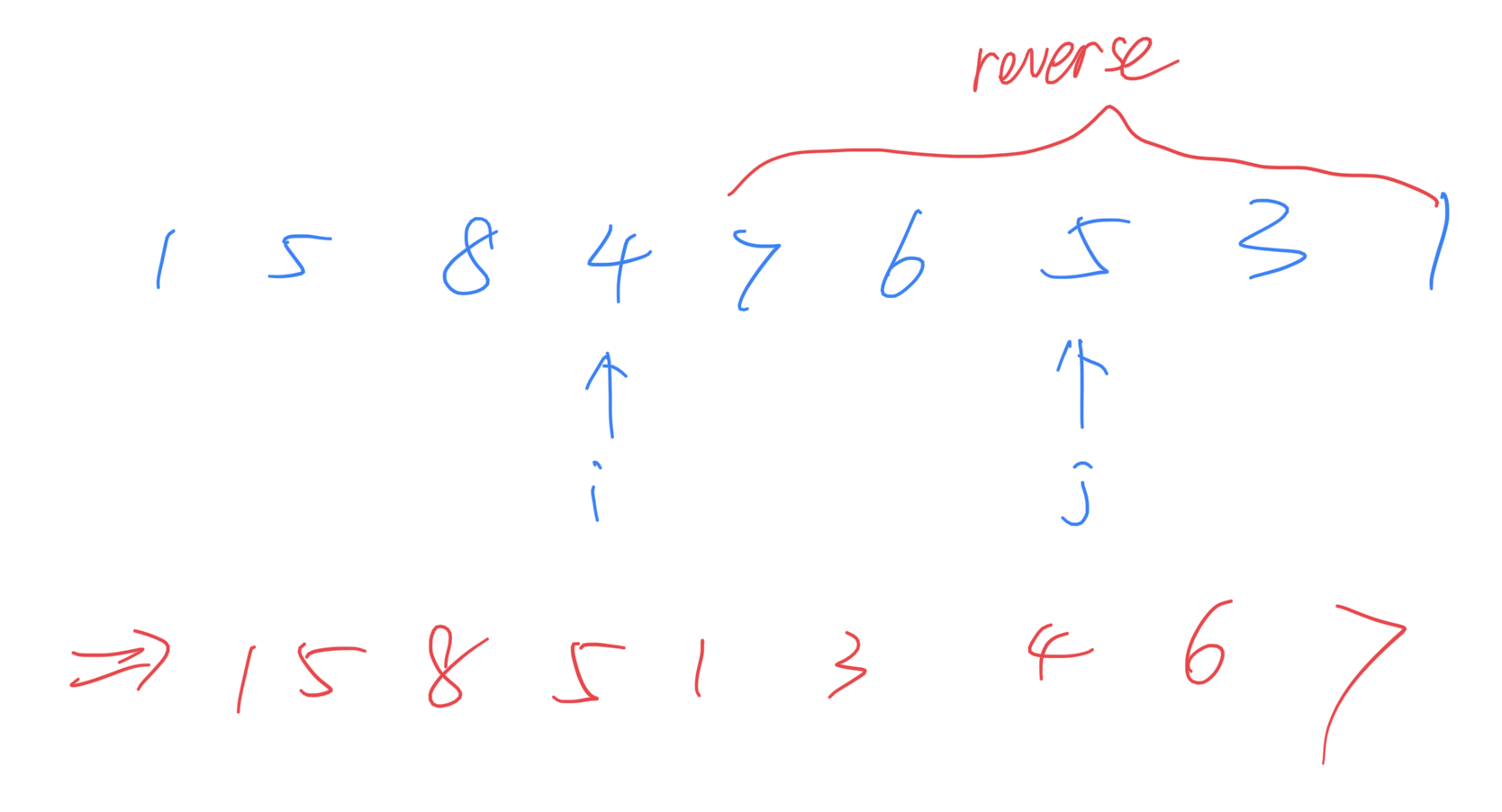
nextlarger

那么为什么这是对的呢？我们以上图为例。

“7 6 5 3 1”不能再大了，因为已经是降序排列。所以只能让”1 5 8 4“变大。
我们要求”最小的 比当前数字大的数字“。所以”1 5 8 4“中，让”4“变大是最好的。
当然，”4“也要尽量少变大一些。所以在右边选最小的比4大的元素然后交换。
显然，这个时候i的右边还是降序的。所以右边部分reverse一下就变最小了。

字符串

字符串也是老大难了，那些没什么技术含量（大嘘）又特别烦的题基本是字符串。我做匹配基本就只会双指针，但是我看到httpserver是用自动机做的。所以自动机应该会有用..probably？

自动机

剑指 Offer 20. 表示数值的字符串

主要idea还是好理解的。指针走到某个字符就可能触发一个状态转换。

子串匹配：字符串哈希

虽然讲到子串匹配大家都会想到KMP，但我发现字符串哈希的做法更好理解。

而且lc评论区的这个做法比acwing的更好，下标不用从1开始了，特殊情况在get函数里面处理。

using ULL = unsigned long long;
static const int N = 5e4 + 10;
ULL base = 13331;
ULL f1[N], f2[N], power[N];
ULL get(int l, int r) {
    if (l == 0) return f1[r];
    return f1[r] - f1[l - 1] * power[r - l + 1];
}
int strStr(string s, string p) {
    if (p.empty()) return 0;
    power[0] = 1;
    for (int i = 1; i < N; i++) power[i] = power[i - 1] * base;

    int m = s.size(), n = p.size();
    f1[0] = s[0];
    for (int i = 1; i < m; i++) {
        f1[i] = f1[i - 1] * base + s[i];
    }
    f2[0] = p[0];
    for (int i = 1; i < n; i++) {
        f2[i] = f2[i - 1] * base + p[i];
    }
    for (int i = 0; i + n - 1 < m; i++) {
        if (get(i, i + n - 1) == f2[n - 1]) return i;
    }
    return -1;
}

子串匹配：KMP

恶心人

273. 整数转换英文表示

这题要把握住三个一组来处理。把”处理三位“抽象出一个函数来做。

Excel表列

Lc168

这个题第二次做还是8会。所以必须得搞清楚原理。

题干是实现1->A, 2->B, …, 26->Z, 27->AA这样的转化。

马上想到进制转换；这个pattern相当于每过26个字母就进一位。

不妨先思考一下更简单的反向问题（lc171）。可以发现AA = A * 26 + A = 27. 所以每位上都是字母*26的幂？！

int titleToNumber(string s) {
    int cur = 0;
    for (char c : s) {
        cur = cur * 26 + (c - 'A' + 1);
    }
    return cur;
}

做完反向问题再去做原问题，可以每次解析出最后一个字母。

拿10进制做类比：比如198，先%10解析出最后一位“8”，添加到结果，原数字减去8变成190，再/=10变成19，继续重复。

这里比如27，先%26解析出最后一位“1”，也就是“A”，添加到结果，原数字减去1变成26，再/=26变成1，继续重复。结果是“AA”。

坑在于%26的结果如果是0的话，其实是“Z”。所以特判一下就可以了。

string convertToTitle(int x) {
    string res;
    while (x) {
        int cur = x % 26;
        if (!cur) cur = 26; // 最后一位是Z
        res += ('A' + cur - 1);
        x -= cur; // 减去最后一位
        x /= 26;
    }
    reverse(res.begin(), res.end());
    return res;
}

数学

记录一些如果没做过绝对做不出的题。

89. 格雷编码

这题是递推，设已经有了n阶格雷码的集合，要得到(n+1)阶。

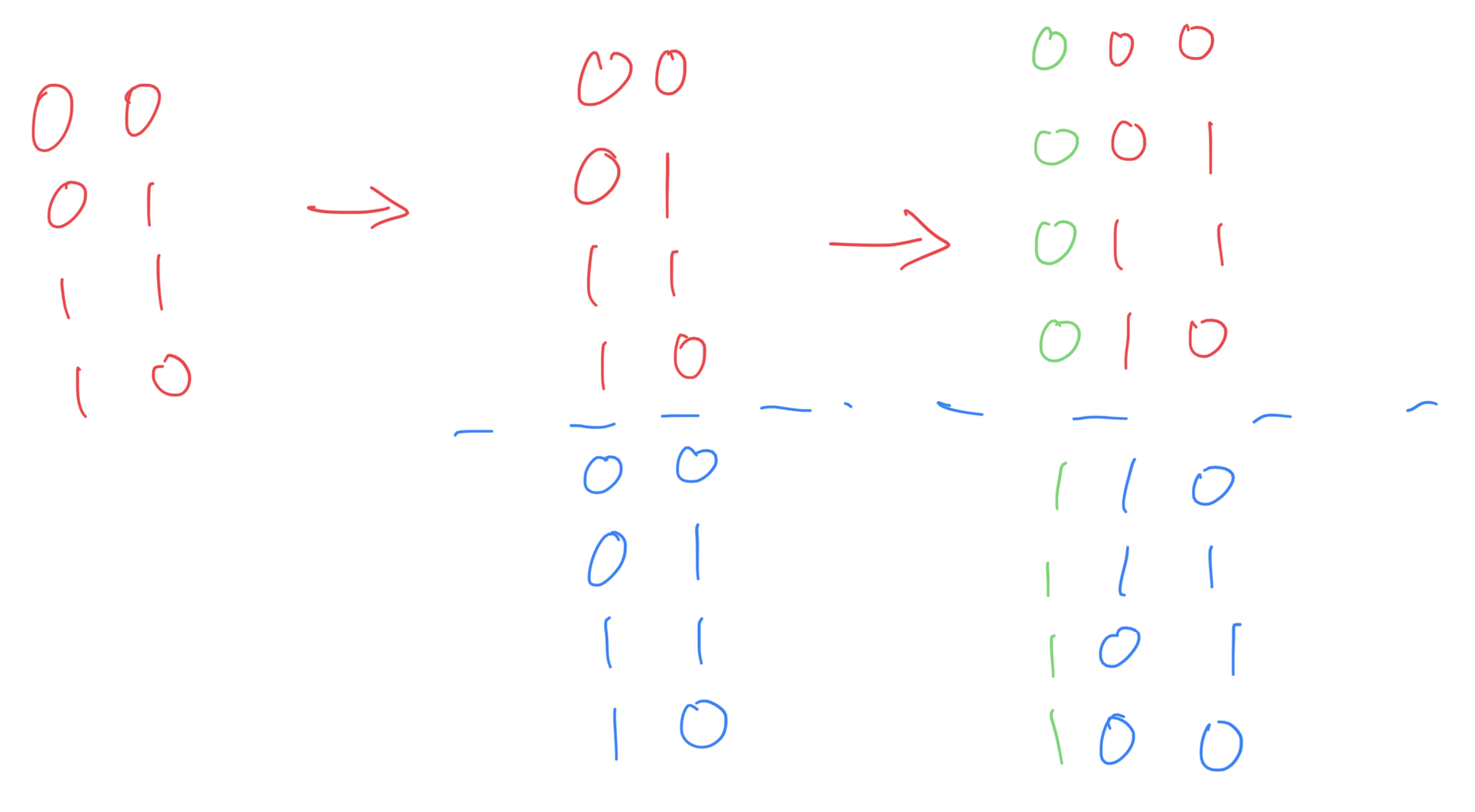
观察到G(n+1)的元素个数是G(n)的两倍。所以将G(n)的元素复制一份，元素个数就相等了。
发现把复制的那份倒置，除了中间衔接处不满足格雷编码条件，其他都满足了。
在复制的那份前面整体加一位1，就得到G(n+1)了。

图示，以G(2)->G(3)为例：

gray

172. 阶乘后的零

可以发现0只能由2和5的因子组合而成。而出现5肯定已经出现2，所以问题转化为“从1到n中有多少个5的因子”。

暴力 O(n^2)

for (int num = 1; num <= n; i++) {
  while (num % 5 == 0) {
    num /= 5; cnt++;
  }
}

记忆化 O(n) 可AC

int getFives(int num) {
  while (num % 5 == 0) {
    num /= 5; cnt++;
  }
}

旋转数组相关问题

189.轮转数组

要求原地将数组旋转k次。这个题没做过的话是真的不会。我做了三遍才知道怎么做。

比如

[1,2,3,4,5,6,7]->[5,6,7,1,2,3,4]

其实就是先reverse前一段，再reverse后一段，再整个reverse。如下：

[1,2,3,4,5,6,7]->[4,3,2,1,5,6,7]->[4,3,2,1,7,6,5]->[5,6,7,1,2,3,4]

搜索旋转排序数组，元素不重复

33. 搜索旋转排序数组

153. 寻找旋转排序数组中的最小值

排序数组旋转之后会分成两段，两段都是有序的。

元素不重复的话有一个好处，给到一个数，你就能马上知道这个数在哪一段上（和a[left]比较）。这样只要一直往“中间”走，就能找到分界点。分界点找到之后根据target的值，在两段之一上直接二分就行了。

但“先找到分界点，再二分”其实还是太麻烦了。直接二分就可以了，但要注意什么时候往左什么时候往右。只有接下来的三种情况是往左搜的 (r=mid - 1)。

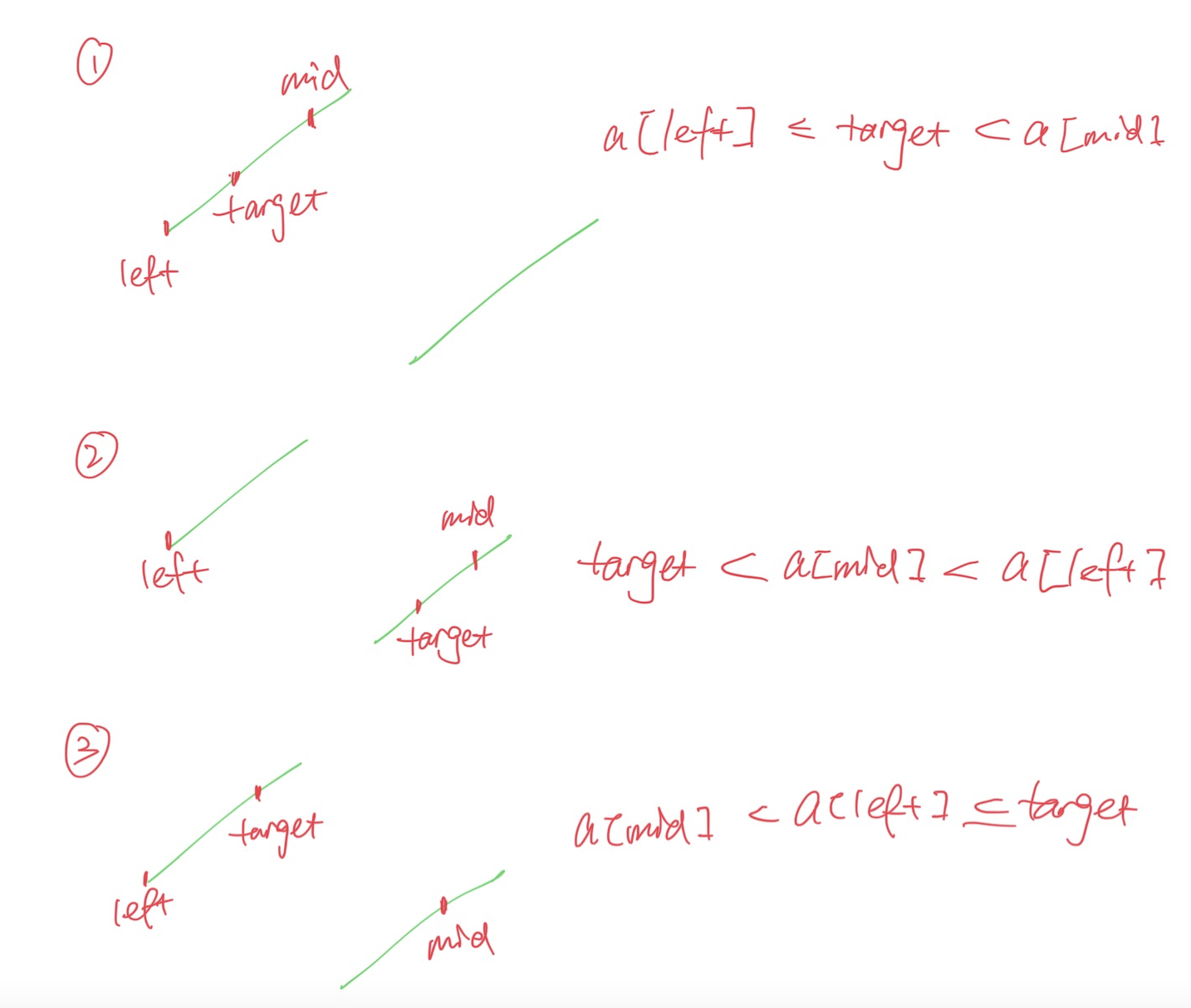
rotate

int search(vector<int>& a, int target) {
    int l = 0, r = a.size() - 1;
    while (l < r) {
        int mid = l + r + 1 >> 1;
        bool cond1 = a[l] <= target, cond2 = target < a[mid], cond3 = a[mid] < a[l];
        if (cond1 && cond2 || cond2 && cond3 || cond3 && cond1) r = mid - 1;
        else l = mid;
    }
    return a[l] == target ? l : -1;
}

搜索旋转排序数组，元素重复

81. 搜索旋转排序数组 II

154. 寻找旋转排序数组中的最小值II

有重复的话，给到一个数，你并不能知道这个数在哪一段上，因为可能出现a[left] == a[mid]的情况。

只需要一直比较a[left]和a[mid]，相等的话让left++，相当于排除一个错误的元素。其他都和无重复的case一样。

最坏时间复杂度是O(n)。

完全一致

bool search(vector<int>& a, int target) {
    int l = 0, r = a.size() - 1;
    while (l < r) {
        int mid = l + r + 1 >> 1;
        if (a[l] == a[mid]) {
            l++; continue;
        }
        bool cond1 = a[l] <= target, cond2 = target < a[mid], cond3 = a[mid] < a[l];
        if (cond1 && cond2 || cond2 && cond3 || cond3 && cond1) r = mid - 1;
        else l = mid;
    }
    return a[l] == target ? true : false;
}

Allen Shao