背包问题2。

完全背包

完全背包和01背包的唯一不同是：每个物品都可以取无限次。

因此在遍历容量j的过程中应该从头开始，而不是01里面的从尾部开始。

518. 零钱兑换 II

dp[j] = coins[0:i]中，能够组成j的子集数量。

按照01背包中494的套路，改成完全背包就可以。

def change(self, amount: int, coins: List[int]) -> int:
    dp = [1] + [0]*amount
    for i in range(len(coins)):
        for j in range(coins[i], amount+1):
            dp[j] += dp[j-coins[i]]
    return dp[-1]

注意这里是物品在外层遍历，背包容量在内层遍历。这样的话最后的所有子集中元素都是按coins数组中出现的顺序来排列。

377. 组合总和 Ⅳ

本题的子集中元素可以交换顺序，因此我们需要背包容量在外层遍历，物品在内层遍历，这相当于对于每个容量j，都会把小于j的所有元素一一加入之前的所有子集中，所以顺序就不是严格的。可以看下图：

377

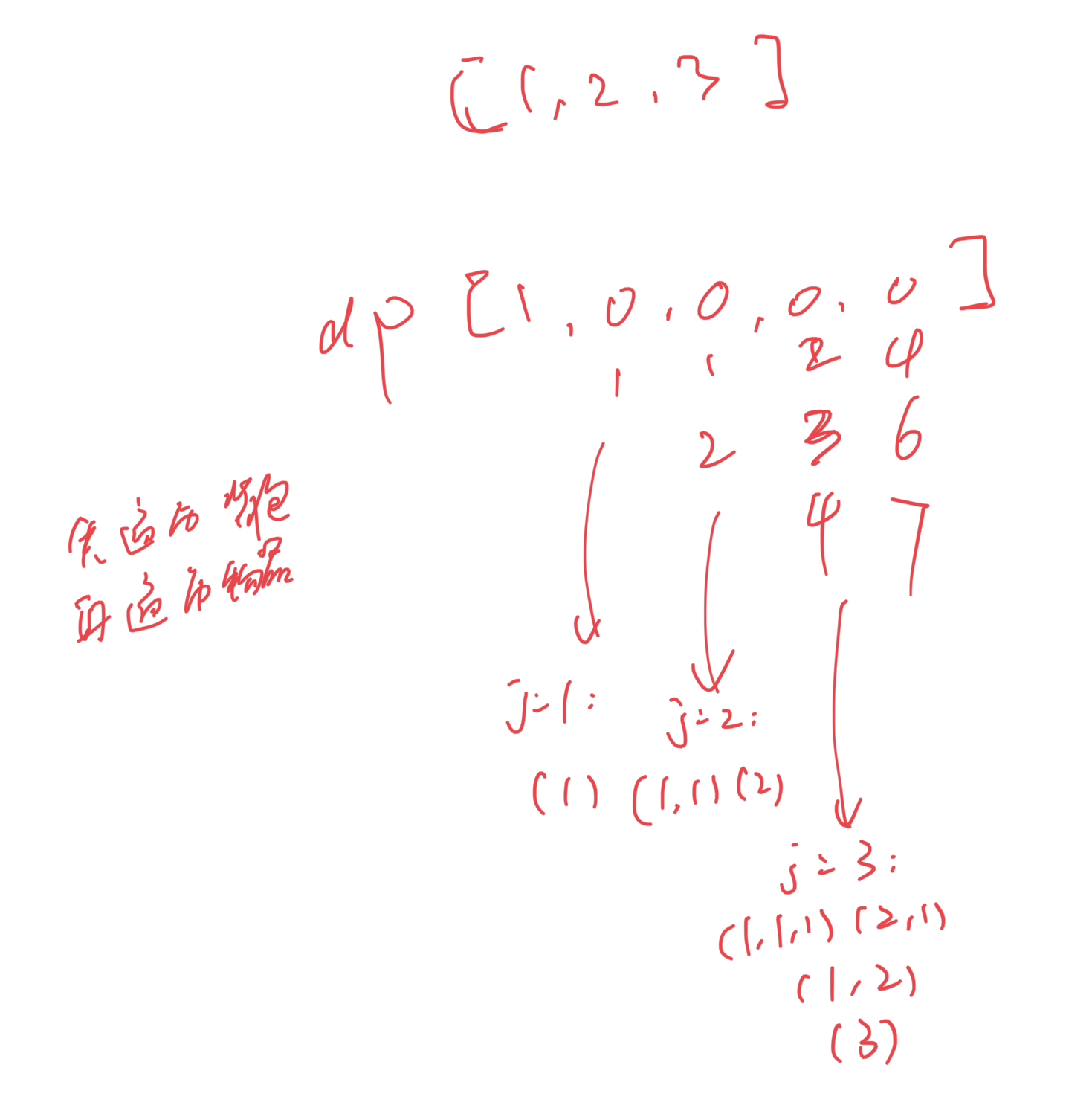
def combinationSum4(self, nums: List[int], target: int) -> int:
    dp = [1] + [0]*target
    for j in range(1, target+1):
        for i in range(len(nums)):
            if nums[i] <= j: dp[j] += dp[j-nums[i]]
    return dp[-1]

代码基本和上一题一样。

322. 零钱兑换

一看就是完全背包，但初始化要想一下。

def coinChange(self, coins: List[int], amount: int) -> int:
    dp = [0] + [inf]*amount
    for value in coins:
        for j in range(value, amount+1):
            dp[j] = min(dp[j], dp[j-value]+1)
    return -1 if dp[-1] == inf else dp[-1]

279. 完全平方数

Same thing.

def numSquares(self, n: int) -> int:
    maximum = math.floor(math.sqrt(n))
    dp = [0] + [inf]*n
    for i in range(1, maximum+1):
        for j in range(i*i, n+1):
            dp[j] = min(dp[j], dp[j-i*i]+1)
    return dp[-1]

139. 单词拆分

dp[j]: s[0:j]是否可以被字典组成，且结尾为i这个词。

注意本题要把背包放在外层，物品放在里层，不然无法handle形如”applepenapple”+[“apple”,”pen”]的情形（处理apple的时候是false，因为pen还没处理；处理pen的时候又走不到最后）。

def wordBreak(self, s: str, wordDict: List[str]) -> bool:
    dp = [1] + [0] * (len(s))
    for j in range(1, len(s)+1):
        for i in wordDict:
            if len(i) <= j:
                match = s[j-len(i):j]
                dp[j] = max(dp[j], dp[j-len(i)]+len(i) if dp[j-len(i)] and match == i else 0)
    return dp[-1] > 0

总结

背包问题基本都可以用回溯+memoization做，它终究还是一个递归问题。

但是要会bottom-up用dp数组来做。对于完全背包，还要注意背包和物品哪个放在外层的问题。