背包问题。

01背包

之所以叫01背包，是因为每个物品只有拿或不拿两个状态。

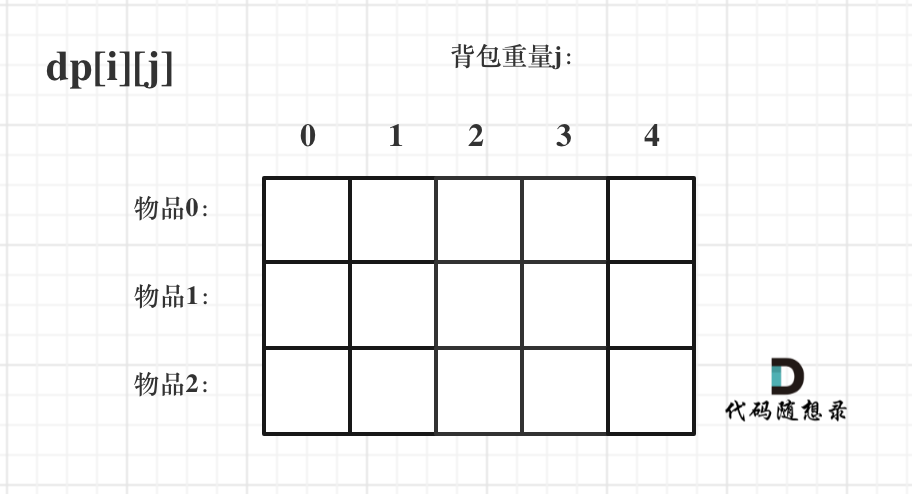
01knapsack

做一个二维数组dp，i表示拿不拿第i个物品，j表示背包容量。每个节点两种情况：

遍历顺序是左上角到右下角（上图中手动画一根对角线）。

是不是很简单呢。

01背包的一维写法

01k2

注意：之所以可以坍缩成一维，是因为二维中每一行i都只与前一行i-1相关。

牢记1：dp[j] = 容量为j的背包在前i个物品中挑选，能够装载的最大值。这里的i不在dp数组里，而是在外循环中。

牢记2：二维数组的做法要初始化第一行(i=0)和第一列(j=0)，但是一维数组只需要初始化第一列就可以。i=0的情况包含在了i的取值范围中了。

416. 分割等和子集

转换问题（很关键）：搜索和等于sum/2的子集，搜索到了就返回true。

可以用回溯+memoization，或者0-1背包bottom-up来做。每个元素的weight和value都是元素本身。

1049. 最后一块石头的重量 II

这题完全想不出怎么转换问题，无奈了。

转换问题：将石头尽量分成重量相同的两堆，这样对撞起来会剩得最少。

0-1背包，容量=sum(stones)//2。每个元素的weight和value都是元素本身。

小结

这两道题其实第一眼很难做，第二眼也很难把它转换成标准的0-1背包来做。但是通过模板+每个元素的weight和value都是元素本身这样的settings，很轻松就可以写出来了。上面两题的套路完全一样，只不过最后对dp输出的处理，416是判断dp[-1][-1]是否等于target，1049是return sum-2*dp[-1][-1]。

另外还需要理解一维数组这个优化。优化之后代码量会显著减少。

附最佳代码：

416

def canPartition(self, nums: List[int]) -> bool:
    if sum(nums) % 2:
        return False
    target = sum(nums) // 2

    dp = [0] * (target+1)
    for i in range(len(nums)):
        for j in range(target, nums[i]-1, -1):
            dp[j] = max(dp[j], dp[j-nums[i]]+nums[i])
    return target == dp[-1]

1049

def lastStoneWeightII(self, stones: List[int]) -> int:
    target = sum(stones) // 2
    dp = [0] * (target+1)
    for i in range(len(stones)):
        for j in range(target, stones[i]-1, -1):
            dp[j] = max(dp[j], dp[j-stones[i]]+stones[i])
    return sum(stones) - 2*dp[-1]

494. 目标和

这题还是0-1背包，但是之前两题是背包能装多少东西，这一题是背包装东西的方案数量。

当然，转换问题的这步还是最重要的：

假设前面是负号的元素之和为neg，那么前面是正号的元素之和为sum(nums)-neg。因此有等式sum(nums)-neg-neg = target. target和sum(nums)已知，所以问题转换为寻找和为(sum(nums)-target)/2的子集数量。

设dp[i][j] = [0,i]当中和为j的子集数量。

递推公式为dp[i][j] = dp[i-1][j-nums[i]] + dp[i-1][j]. (nums[i]在子集中+nums[i]不在子集中)

那么坍缩到一维数组，递推公式就为dp[j] += dp[j-nums[i]]。

初始化的话，dp[0]应该是1，因为j=nums[i]的情况是有一个子集的。

def findTargetSumWays(self, nums: List[int], target: int) -> int:
    if sum(nums) < abs(target) or (sum(nums)-target) % 2:
        return 0
    t = (sum(nums)-target)//2
    dp = [1] + [0]*t
    for i in range(len(nums)):
        for j in range(t, nums[i]-1, -1):
            dp[j] += dp[j-nums[i]]
    return dp[-1]

474. 一和零

0-1背包，但是装的东西有两个维度：0的数量和1的数量。

dp[j][k] = str[0:i]中，0的数量小于等于j，且1的数量小于等于k的所有子集中，元素最多的子集中的元素个数。

递推：dp[j][k] = max(dp[j-zeros][k-ones] + 1, dp[j][k]), 其中zeros,ones为当前处理元素的0和1的个数。

初始化：初始化为0就可以。

def findMaxForm(self, strs: List[str], m: int, n: int) -> int:
    def getnums(i):
        c = Counter(strs[i])
        return c["0"],c["1"]
    dp = [[0]*(n+1) for _ in range(m+1)]
    for i in range(len(strs)):
        zeros, ones = getnums(i)
        for j in range(m, zeros-1, -1):
            for k in range(n, ones-1, -1):
                dp[j][k] = max(dp[j-zeros][k-ones] + 1, dp[j][k])
    return dp[-1][-1]