贪心4.

452. 用最少数量的箭引爆气球

还是熟悉的区间问题，但这次应该是要求区间的交集。

首先肯定还是排好序，不然东一个西一个不好做。

def findMinArrowShots(self, points: List[List[int]]) -> int:
    points.sort(key=lambda x:x[0])
    lastInterval = [-inf, inf]
    res = 1
    def overlaps(currentInterval):
        nonlocal lastInterval
        s1, e1 = lastInterval[0], lastInterval[1]
        s2, e2 = currentInterval[0], currentInterval[1]
        if s2 > e1:
            lastInterval = currentInterval
            return False
        lastInterval = [max(s1,s2),min(e1,e2)]
        return True
    for i in points:
        if not overlaps(i):
            res += 1
    return res

思路是保持一个最小交集，如果新区间与之前区间的最小交集不重合那就要一支新箭了。

435. 无重叠区间

这题把我带回了MIT6.006的课堂上。当时Devadas让学生举手回答：当两个区间重合的时候应该erase哪一个？结果学生提出的每个方案Devadas都举出了一个反例，给我看乐了。

话说回来，本题的精髓确实是局部最优如何达成，即当两个区间重合的时候应该erase哪一个。答案是：首先，按照开始位置排序整个区间数组。如果currentInterval被lastInterval包围(contain)，那就erase lastInterval。不然就erase currentInterval。你能看出为什么吗？

453

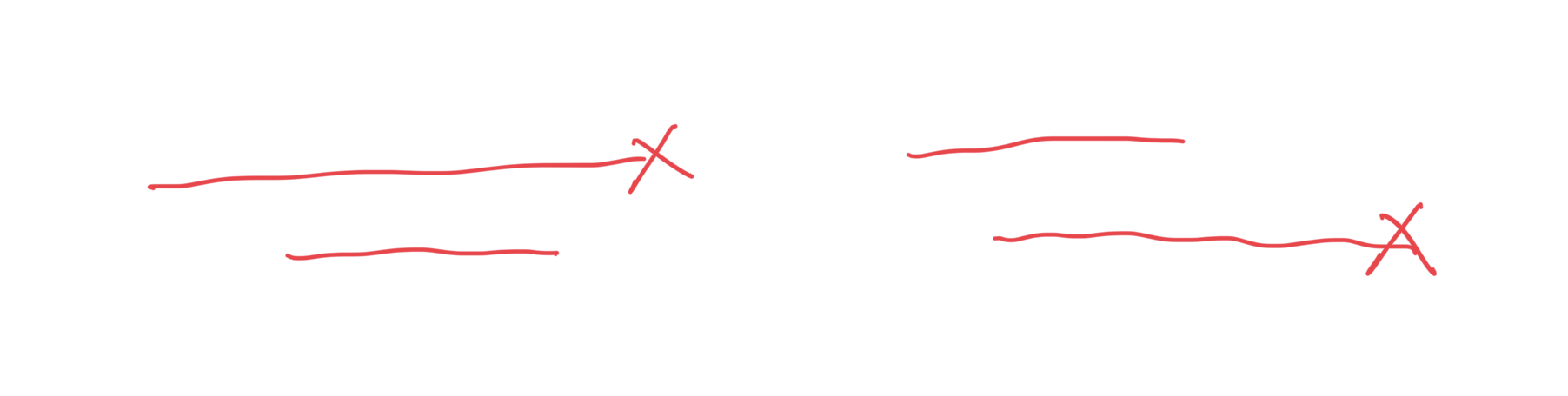
def eraseOverlapIntervals(self, intervals: List[List[int]]) -> int:
    lastInterval = None
    def overlap(i):
        nonlocal lastInterval
        if not lastInterval or lastInterval[1] <= i[0]:
            return False
        return True
    count = 0
    intervals.sort(key=lambda x:x[0])
    for i in intervals:
        if overlap(i):
            if i[1] <= lastInterval[1]:
                lastInterval = i
            count += 1
        else:
            lastInterval = i
    return count

763. 划分字母区间

理解题目限制：如果字母a在区间内，那么区间需要至少延伸到a的最后一次occurrence。

所以这题和之前的跳跃游戏类似，都是要动态更新区间的长度。

763

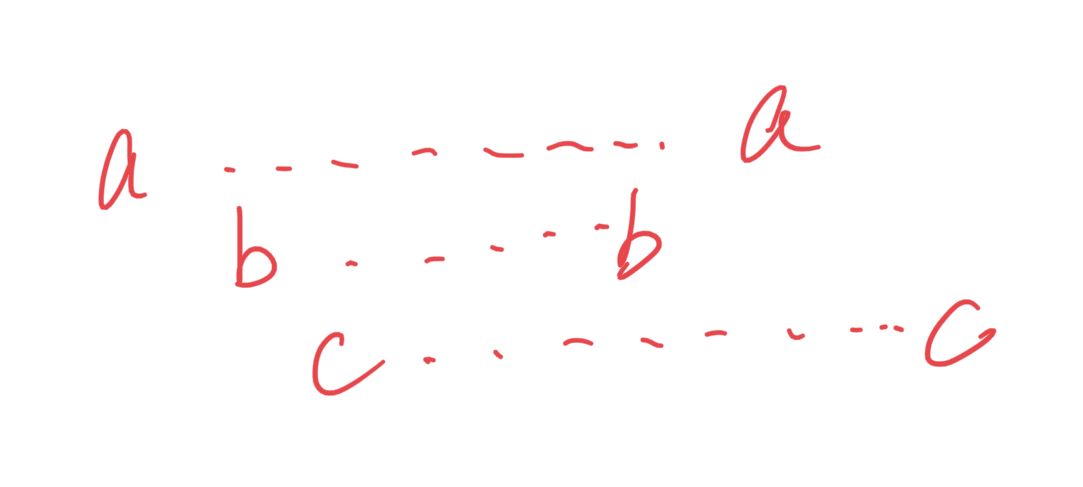
首先找到一个{字母:lastOccurrence}的字典，然后根据上图的逻辑更新区间长度。

def partitionLabels(self, s: str) -> List[int]:
    lastOcc = {}
    for i in range(len(s)-1, -1, -1):
        if s[i] not in lastOcc:
            lastOcc[s[i]] = i
    currentmax = 0
    res = []
    for i in range(len(s)):
        currentmax = max(currentmax, lastOcc[s[i]])
        if i == currentmax:
            res.append(i+1 - sum(res))
    return res

56. 合并区间

如果说452是求区间的交集，那这题就是求区间的并集。思路差不多，关键还是开始时要对区间数组进行排序。

def merge(self, intervals: List[List[int]]) -> List[List[int]]:
    def overlaps(i1, i2):
        if i2[0] > i1[1]:
            return False
        return True
    def merge(i1, i2):
        return [min(i1[0], i2[0]), max(i1[1], i2[1])]

    res = []
    temp = []
    intervals.sort()
    for i in intervals:
        if not temp:
            temp = i
            continue
        if overlaps(temp, i):
            temp = merge(temp, i)
        else:
            res.append(temp)
            temp = i
    if temp:
        res.append(temp)
    return res