贪心2.
122. 买卖股票的最佳时机 II
贪心判断两日价格差值,如果是正数就加入,负数就不管了。
总的来说和之前的摆动序列很像,但是这里我们只关心递增的单调序列。
def maxProfit(self, prices: List[int]) -> int:
sum = 0
prev = inf
for p in prices:
if prev != inf and p > prev:
sum += (p-prev)
prev = p
return sum
55. 跳跃游戏
先理思路,看起来本题只要不跳到0上就都可以到达末尾。
但其实这是一个陷阱,本题和游戏的具体规则关系不大,但人会很自然地纠结于这个规则上面。
实际上我们只关心我最远能跳到哪里,中间怎么跳的我不管。只要最远能跳到数组末尾,那就可以返回True了。
因此代码如下:
def canJump(self, nums: List[int]) -> bool:
maxreachable = 0
i = 0
while i <= maxreachable:
if nums[i]:
maxreachable = max(maxreachable, i+nums[i])
if maxreachable >= len(nums)-1:
return True
i += 1
return False
45. 跳跃游戏 II
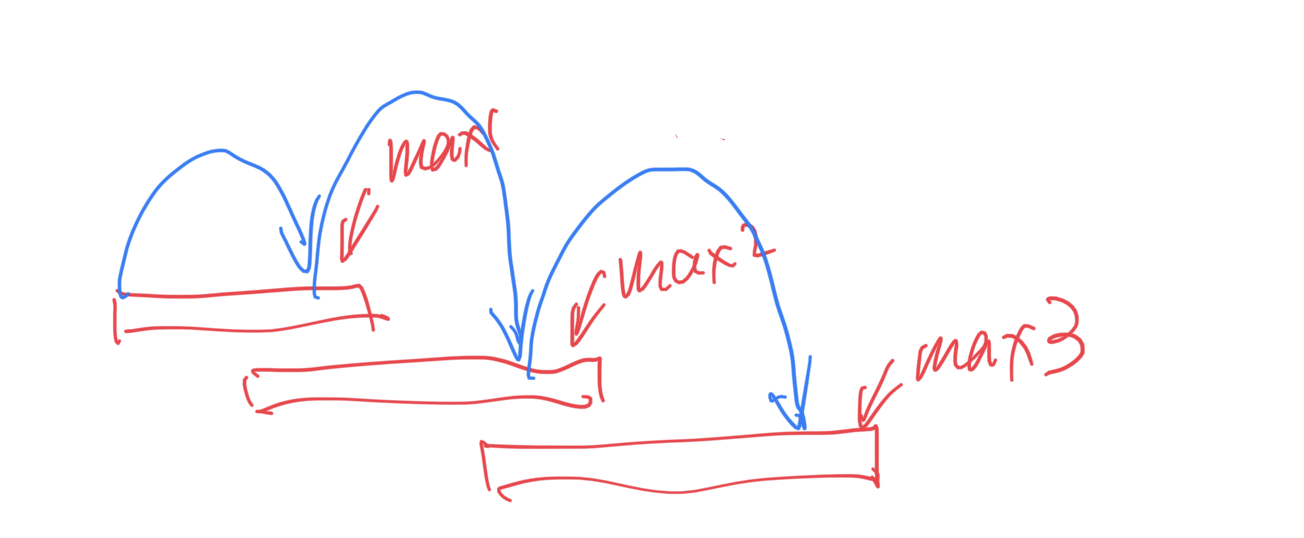
这题思路比较复杂,我是没有想出来。简单来说就是在当前reachable区间遍历的时候会生成下一个reachable区间。如果下一个reachable区间包含了数组的末尾,则终止。总的reachable区间数量就是需要跳跃的次数。
def jump(self, nums: List[int]) -> int:
if len(nums) == 1:
return 0
count = 0
currentMax = 0
nextMax = 0
for i in range(len(nums)):
nextMax = max(nextMax, nums[i]+i)
if i == currentMax:
count += 1
currentMax = nextMax
if nextMax >= len(nums)-1:
break
return count
1005. K 次取反后最大化的数组和
思路很明确:从绝对值大的负数开始把负数反转完,再取最小的正数把剩下的次数反转完。
最优的做法是按照绝对值大小从大到小排列。
def largestSumAfterKNegations(self, nums: List[int], k: int) -> int:
nums.sort(key=lambda x: abs(x), reverse=True)
for i in range(len(nums)):
if k == 0: break
if nums[i] < 0:
nums[i] = -nums[i]
k -= 1
if k % 2:
nums[-1] = -nums[-1]
return sum(nums)