二叉树的构造与修改。
106. 从中序与后序遍历序列构造二叉树
这个题我第一次做的时候一点头绪都没。直接看题解。
这题的重点是明确后序数组的最后一个元素是当前子树的根元素,然后递归解两个子问题。
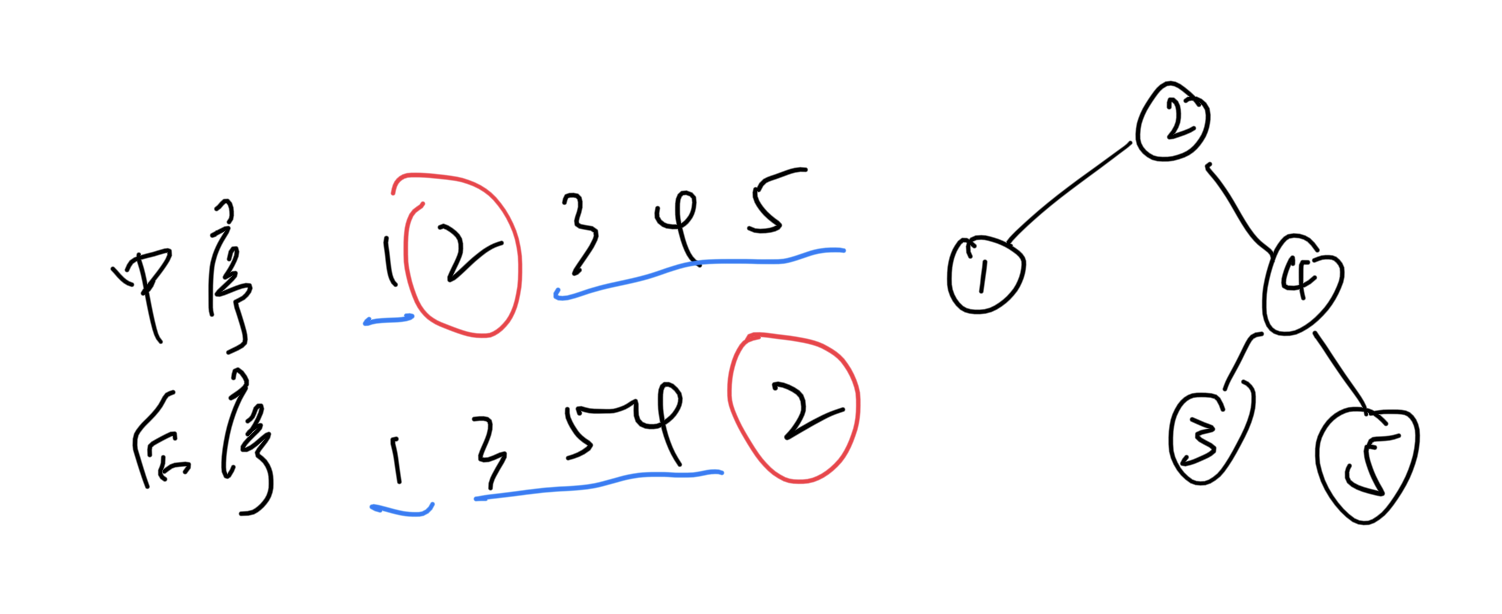
总的来说三步走:找 - 切 - 进入子问题。
找:注意两个特殊情况,即数组为空或只有一个元素,都是可以马上返回的。
切:先切中序,再根据元素的个数切后序。
切完之后就可以进入子问题递归了。
def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode:
if not postorder:
return None
if len(postorder) == 1:
return TreeNode(postorder[0])
# 找
cutpoint = postorder[-1]
# 切
inleft, inright = [],[]
postleft, postright = [], []
for i in range(len(inorder)):
if inorder[i] == cutpoint:
# 注意好下标
inleft, inright = inorder[:i], inorder[i+1:]
postleft, postright = postorder[:i], postorder[i:-1]
# 进入子问题
cur = TreeNode(cutpoint, self.buildTree(inleft, postleft), self.buildTree(inright, postright))
return cur
切的时候注意下标。中左对应后左,中右对应后右,两半的数量要完全一致。
容易看出的优化是传下标而不是复制切片,但这边下标的计算要注意一下。
def helper(inorder, ileft, iright, postorder, pleft, pright):
if pleft > pright:
return None
if pleft == pright:
return TreeNode(postorder[pleft])
# 找
cutpoint = postorder[pright]
# 切
cur = None
for i in range(ileft, iright+1):
if inorder[i] == cutpoint:
print(i)
# 进入子问题
cur = TreeNode(cutpoint, helper(inorder, ileft, i-1, postorder, pleft, pleft+i-1-ileft), helper(inorder, i+1, iright, postorder, pleft+i-ileft, pright-1))
return cur
return helper(inorder, 0, len(inorder)-1, postorder, 0, len(postorder)-1)
注意pleft+i-1-ileft这里。仔细想想其实并不复杂。
105. 从前序与中序遍历序列构造二叉树
有了上一题的基础,这一题并不复杂,按照前序的第一个元素切就可以了。
617. 合并二叉树
递归做法很简单,子问题是分别合并左右子树:
def mergeTrees(self, root1: TreeNode, root2: TreeNode) -> TreeNode:
if not root1 and not root2:
return None
if root1 and not root2:
return root1
if root2 and not root1:
return root2
return TreeNode(root1.val+root2.val, self.mergeTrees(root1.left, root2.left), self.mergeTrees(root1.right, root2.right))
迭代的话可以参照之前对称那题。思路是将两个树对应的节点成对地push进队列中。
def mergeTrees(self, root1: TreeNode, root2: TreeNode) -> TreeNode:
if not root1:
return root2
if not root2:
return root1
queue = deque([root1, root2])
while len(queue) > 0:
left = queue.popleft()
right = queue.popleft()
left.val += right.val # 以left为本位
if left.left and right.left:
queue.append(left.left)
queue.append(right.left)
if left.right and right.right:
queue.append(left.right)
queue.append(right.right)
if not left.left and right.left:
left.left = right.left
if not left.right and right.right:
left.right = right.right
return root1
注意该解法是以left为本位的,只要把left缺少的用right填充就可以了。