这篇主要是二叉树的一些性质。
101. 对称二叉树
这里递归的话要注意子问题并不在一个子树里面,而是“左边的左”vs“右边的右”。这点还是挺迷惑的。
递归:
def isSymmetric(self, root: TreeNode) -> bool:
def compare(left, right):
if left and not right or right and not left:
return False
if not left and not right:
return True
if left.val != right.val:
return False
return compare(left.left, right.right) and compare(left.right, right.left)
if not root:
return False
return compare(root.left, root.right)
迭代的话思路也差不多:
def isSymmetric(self, root: TreeNode) -> bool:
def compare(left, right):
if left and not right or right and not left:
return False
if not left and not right:
return True
if left.val != right.val:
return False
return True
if not root:
return False
queue = deque([root.left, root.right])
while len(queue):
left = queue.popleft()
right = queue.popleft()
if not compare(left, right):
return False
if left:
queue.append(left.left)
queue.append(right.right)
queue.append(left.right)
queue.append(right.left)
return True
注意从queue中pop的时候要一对一对取出。
n叉树的最大/最小深度
最大深度
递归:
maxdepth(node) = 1 + max(maxdepth(node.left) + maxdepth(node.right))
迭代:
层序遍历之后取层数。
最小深度
递归:
注意终点需要是叶子结点,即没有左右孩子的节点。将该条件要加入递归的base case中即可。
def minDepth(self, root: TreeNode) -> int:
if not root:
return 0
if not root.left and not root.right:
return 1
left = self.minDepth(root.left) if root.left else inf
right = self.minDepth(root.right) if root.right else inf
return min(left, right) + 1
迭代:
还是层序,取第一个碰到的没有孩子的节点的深度。
二叉树节点的数量
递归
数量(node) = 数量(node.left) + 数量(node.right) + 1
迭代
层序
完全二叉树
方法1
判断:如果以当前节点为根的树是满二叉树,那就能直接算出来了。
判断方法:左边走到底和右边走到底的深度是不是一样。
def countNodes(self, root: TreeNode) -> int:
if not root:
return 0
lh = 0
rh = 0
l = root
r = root
while l:
lh += 1
l = l.left
while r:
rh += 1
r = r.right
if lh == rh:
return 2 ** lh - 1
return self.countNodes(root.left) + self.countNodes(root.right) + 1
时间复杂度据称是O(log^2n),但是我也推不出来。
方法2:二分查找+位运算
这个还算好理解,对最底层的n/2个node做二分查找,然后判断目标node是否存在。
判断方法:
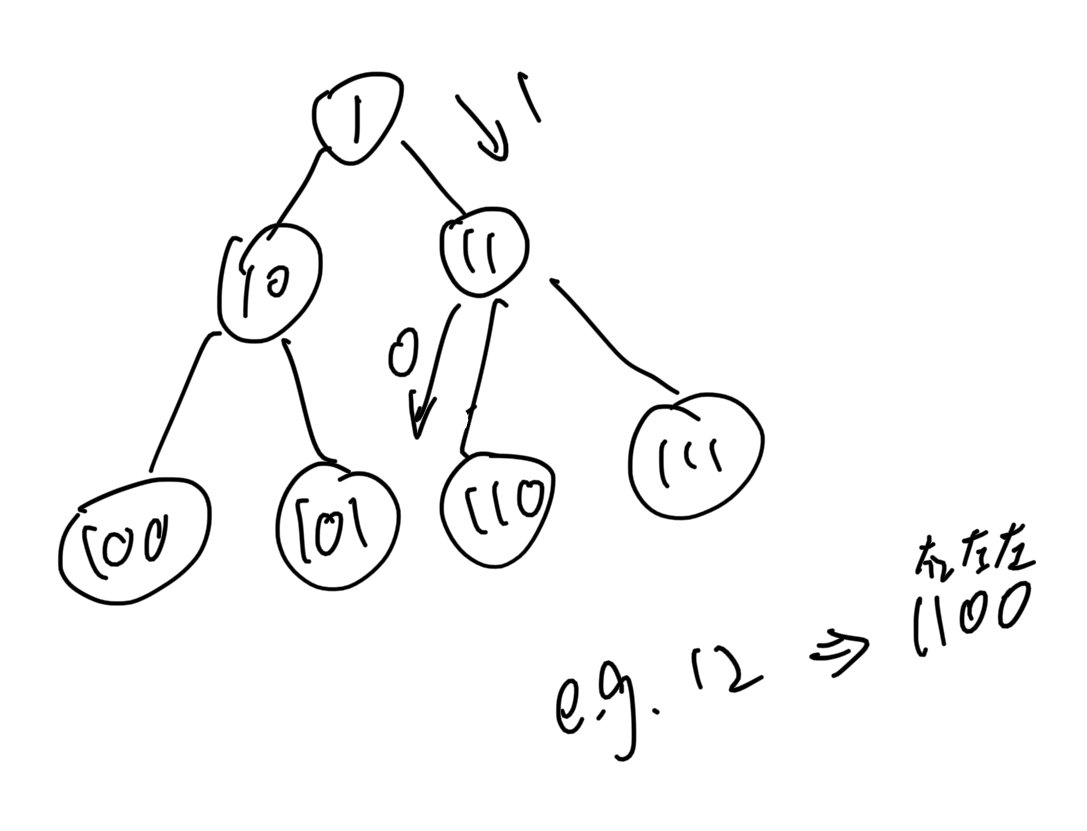
def countNodes(self, root: TreeNode) -> int:
if not root:
return 0
lh = 0
l = root
while l:
lh += 1
l = l.left
if lh == 1:
return 1
lo = 2 ** (lh-1)
hi = 2 ** lh - 1
best = 0
while (lo <= hi):
mid = (lo + hi) // 2
pairnum = 1 << (lh - 2)
cur = root
for _ in range(lh-1):
if pairnum & mid > 0:
cur = cur.right
else:
cur = cur.left
pairnum = pairnum >> 1
if cur:
lo = mid + 1
best = mid
else:
hi = mid - 1
return best
二叉树是否平衡 110. 平衡二叉树
容易想到自顶向下的递归,但是显然很多height被重复调用了。
回想在CLRS中,算AVL的时候也用到了检查平衡的函数。当时是augment了treenode,加入了height属性。但现在做不到。
题解的思路是让底端的nodes把自己“是否平衡”这一信息体现在返回值里面,这样就不用递归调用isBalanced()了。
def isBalanced(self, root: TreeNode) -> bool:
def height(root):
if not root:
return 0
lh = height(root.left)
rh = height(root.right)
if lh == -1 or rh == -1 or not -1<=lh-rh<=1:
return -1
return max(height(root.left),height(root.right)) + 1
return height(root) >= 0
257. 二叉树的所有路径
第一个想到的就是有向图dfs用栈,碰到叶子的时候输出路径。
def binaryTreePaths(self, root: TreeNode) -> List[str]:
res = []
stack = []
def dfs(root):
stack.append(root)
if not root.left and not root.right:
res.append("->".join(map(lambda x: str(x.val),stack)))
if root.left:
dfs(root.left)
if root.right:
dfs(root.right)
stack.pop()
dfs(root)
return res
当然用递归也行,但感觉没这个直观,还要传一个半成品的path参数。