二叉树也是面试的高频考察点。

遍历

主要还是讲一下迭代法。递归三种遍历都差不多，很简单。

前序

def preorderTraversal(self, root: TreeNode) -> List[int]:
    if not root:
        return []
    stack = [root]
    res = []
    while len(stack) > 0:
        cur = stack.pop()
        res.append(cur.val)
        if cur.right:
            stack.append(cur.right)
        if cur.left:
            stack.append(cur.left)
    return res

这里有一个点是要先将右孩子加入栈再加入左孩子，这样pop的时候才是左孩子优先。

注意：二叉树的遍历和图的遍历完全不是一个概念，除了层序遍历=BFS。

中序

思路是使用null节点来判断是否应该处理当前节点。

中序遍历是左 - 右 - 中，所以先一路向左，碰到null就说明当前分支左边走完了，这时pop处理左边最底端的节点，接着向右处理。因为每个节点只会被加入栈一次（在parent向左遍历的过程中），所以不会重复。

def inorderTraversal(self, root: TreeNode) -> List[int]:
    if not root:
        return []
    stack = []
    res = []
    cur = root
    while cur or len(stack) > 0:
        if cur:
            stack.append(cur)
            cur = cur.left
        else:
            cur = stack.pop()
            res.append(cur.val)
            cur = cur.right
    return res

后序

后序又不一样了。左-右-中，反过来是中-右-左；后面两个再反一下就是中-左-右，前序遍历。因此后序是可以通过前序来推的。

def postorderTraversal(self, root: TreeNode) -> List[int]:
    if not root:
        return []
    stack = [root]
    res = []
    while len(stack) > 0:
        cur = stack.pop()
        res.append(cur.val)
        if cur.left:
            stack.append(cur.left)
        if cur.right:
            stack.append(cur.right)
    return list(reversed(res))

遍历的统一写法

要统一写法，思路和之前的中序一样，仍然是使用null节点。

基本操作：

以中序遍历为例：

def inorderTraversal(self, root: TreeNode) -> List[int]:
    if not root:
        return []
    stack = [root]
    res = []
    while len(stack) > 0:
        cur = stack.pop()
        if cur:
            if cur.right:
                stack.append(cur.right)
            stack.append(cur)
            stack.append(None)
            if cur.left:
                stack.append(cur.left)
        else:
            cur = stack.pop()
            res.append(cur.val)
    return res

层序遍历

层序的话用迭代更方便，因此介绍一下递归的写法。

递归的话一定要在参数中加depth。

def levelOrder(self, root: TreeNode) -> List[List[int]]:
    res = []
    def helper(root, depth):
        if not root: return []
        if len(res) == depth: res.append([]) # start the current depth
        res[depth].append(root.val) # fulfil the current depth
        if  root.left: helper(root.left, depth + 1) # process child nodes for the next depth
        if  root.right: helper(root.right, depth + 1)
    helper(root, 0)
    return res

顺便也贴一个用deque的写法：

def lvlOrder(root):
    queue = deque([root])
    res = []
    while (len(queue)>0):
        size = len(queue)
        temp = []
        for _ in range(size):
            cur = queue.popleft()
            temp.append(cur.val)
            if cur.left:
                queue.append(cur.left)
            if cur.right:
                queue.append(cur.right)
        res.append(temp)
    return res

116. 填充每个节点的下一个右侧节点指针

容易想到层序遍历，但是挑战常数空间就要换个思路了。

递归思路：假设当前层已经用next指针连好了，怎么样让下一层也用next指针连好？

116

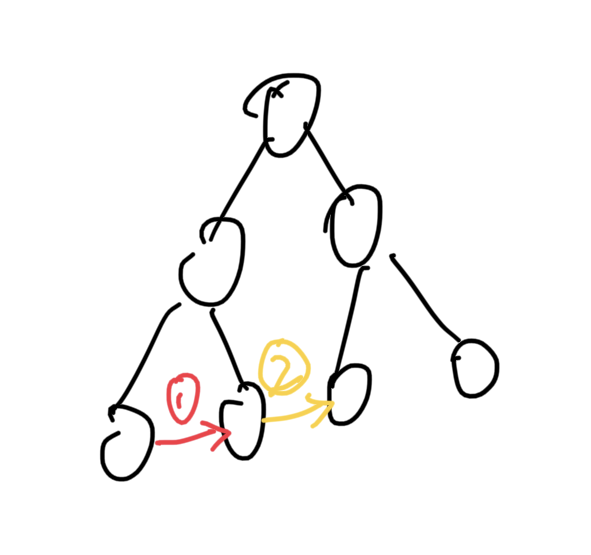
根据两种next ptr类型，可以写出如下递归代码：

def connect(self, root: 'Node') -> 'Node':
    if not root:
        return None
    if root.left:
        root.left.next = root.right
        if root.next:
            root.right.next = root.next.left
        self.connect(root.left)
        self.connect(root.right)
    return root

117. 填充每个节点的下一个右侧节点指针 II

与之前的不同是要追踪一个last节点。

def link(self, last, leftmost, cur):
    if not last:
        last = cur
        leftmost = cur
    else:
        last.next = cur
        last = cur
    return (last, leftmost)

def connect(self, root: 'Node') -> 'Node':
    last = None
    leftmost = root
    while leftmost:
        cur = leftmost
        leftmost = None
        while cur:
            if cur.left:
                last, leftmost = self.link(last, leftmost, cur.left)
            if cur.right:
                last, leftmost = self.link(last, leftmost, cur.right)
            cur = cur.next
        last = None
    return root

注意python函数是pbv的，所以函数返回之后要重新赋值。