字符串相关。
从结构上来说字符串和数组是一样的。所以很多字符串操作和之前讲过的数组也很像(比如双指针)。
344. 反转字符串
交换对应的元素就行,思路没什么好说的。很快写出第一版:
def reverseString(self, s: List[str]) -> None:
for i in range(len(s)//2):
s[i], s[len(s)-1-i] = s[len(s)-1-i], s[i]
但其实还有优化空间:双指针。之前还得算range里的值什么的,要思考一下。双指针直接无需思考。
def reverseString(self, s: List[str]) -> None:
i = 0
j = len(s) - 1
while i < j:
s[i], s[j] = s[j], s[i]
i += 1
j -= 1
541. 反转字符串 II
注意python切片做左值的时候是引用,做右值的时候是copy。
注意python的字符串是immutable的。要做元素操作时先转换成list,最后再reduce一下即可。
这题两种思路,一种的窗口以k为单位,另一种窗口以2k为单位。先看一下一样的部分:
def reverse(s, left, right):
while left < right:
s[left], s[right] = s[right], s[left]
left += 1
right -= 1
def concat(s1, s2):
return s1+s2
一个reverse helper,还有一个后面输出用的reduce function。
以k为单位滑动(我的第一版解法):
def reverseStr(self, s: str, k: int) -> str:
slist = list(s)
left = 0
right = k - 1
while right <= len(s) - 1:
# (left // k) % 2 是偶数,代表要reverse当前窗口。
if not (left // k) % 2:
reverse(slist, left, right)
left += k
right += k
if not (left // k) % 2:
reverse(slist, left, len(s)-1)
return reduce(concat,slist)
可以看到,以k为单位进行操作,隔k进行翻转,只要加个判断条件就行。
另一种操作是以2k为单位操作:
def reverseStr(self, s: str, k: int) -> str:
res = list(s)
for cur in range(0, len(s), 2 * k):
res[cur: cur + k] = reverse(res[cur: cur + k])
这里要注意python切片如果是左值的话就是引用,是右值的话就是copy。
显然这一版省去了很多条件判断,更为简洁。
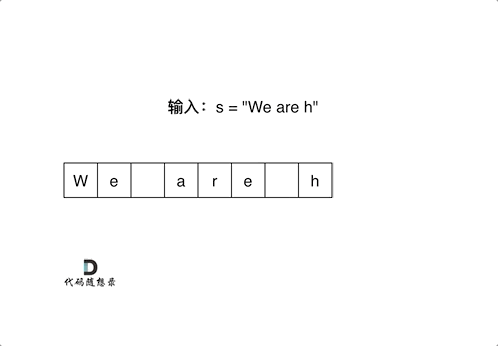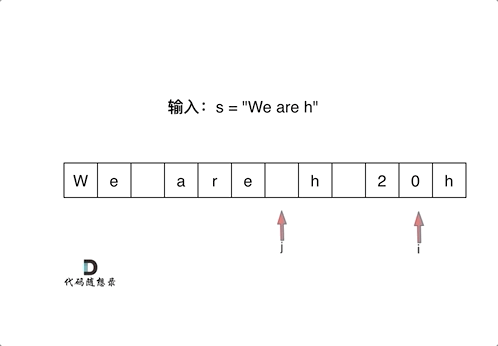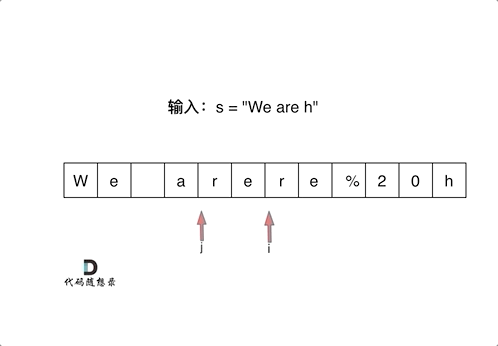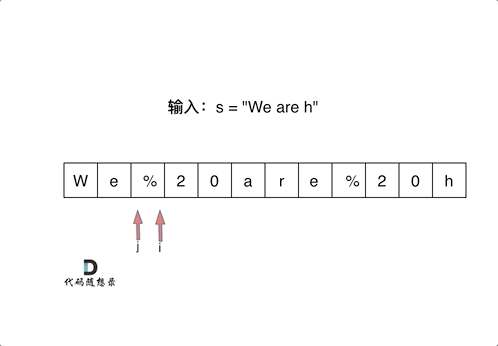
剑指 Offer 05. 替换空格
挑战:in-place替换空格。
数组填充类型的题目,可以先尾部扩容,再从后向前双指针。
151. 翻转字符串里的单词
好题,非常综合。
作为一个medium题,本题主要需要完成两个任务:去除多余的空格,以及翻转单词。
去除多余空格当然可以用内置函数来做,但就没意思了。这个任务可以用之前数组(2)中的双指针来做。
翻转单词可以分为两步:整体翻转,然后每个单词再翻转。
整体的代码量还是比较多的,是一个很好的挑战。
剑指 Offer 58 - II. 左旋转字符串
做过了上一题,这题应该不难:同样是整体反转+局部反转的思路。
KMP
前缀表的概念
对于某个模式字符串s,π(i)表示:s[0, i]中如果有相同的真前缀和真后缀,该真前缀的长度。
其中真前缀 = 不等于自身的前缀。
前缀表的用处
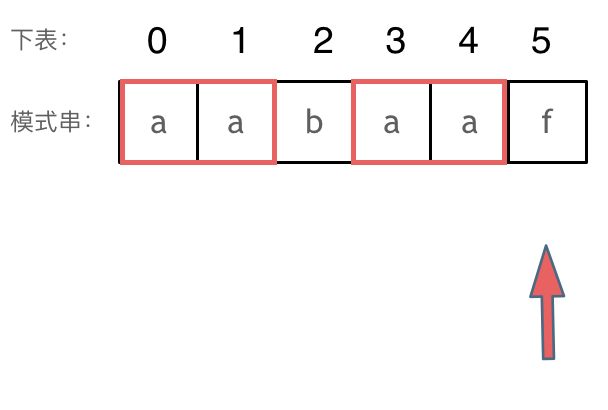
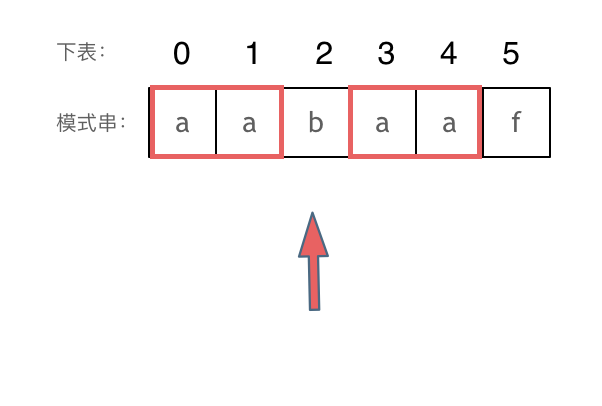
比如说aabaaf的π(5)就是2,因为前缀=后缀=aa。这个时候如果在f处发现不匹配,可以跳到b处继续开始匹配,因为aaf和aab的前缀都是aa。
利用前缀表进行匹配的例子如图所示。
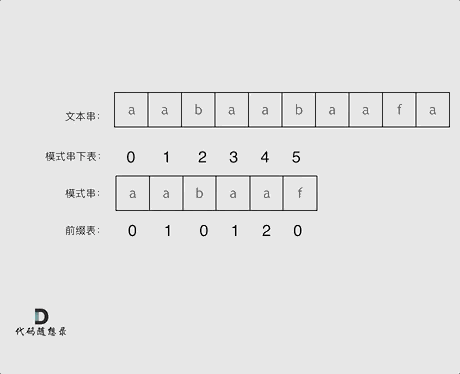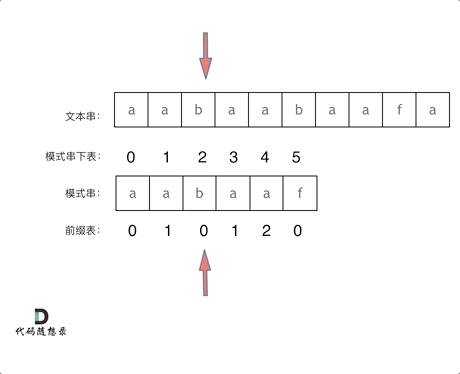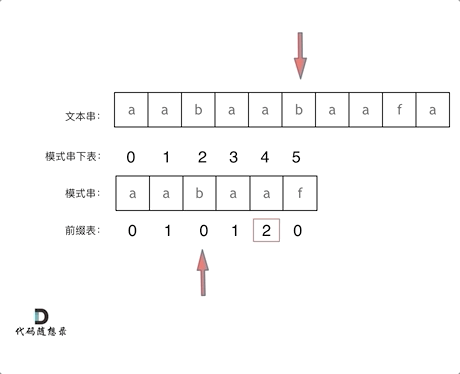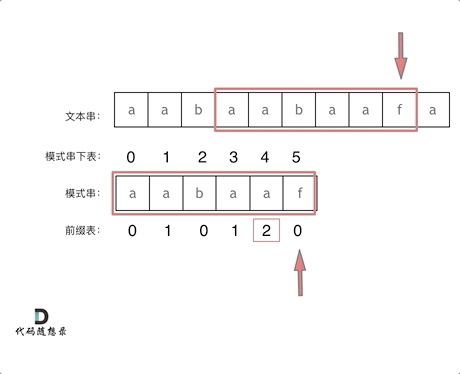
那么目前的问题就是两步走:
- 构建前缀表。
- 通过前缀表做匹配解决问题。
构建前缀表
构建前缀表有点搞,我想了很久。
先讲一下怎么构建:
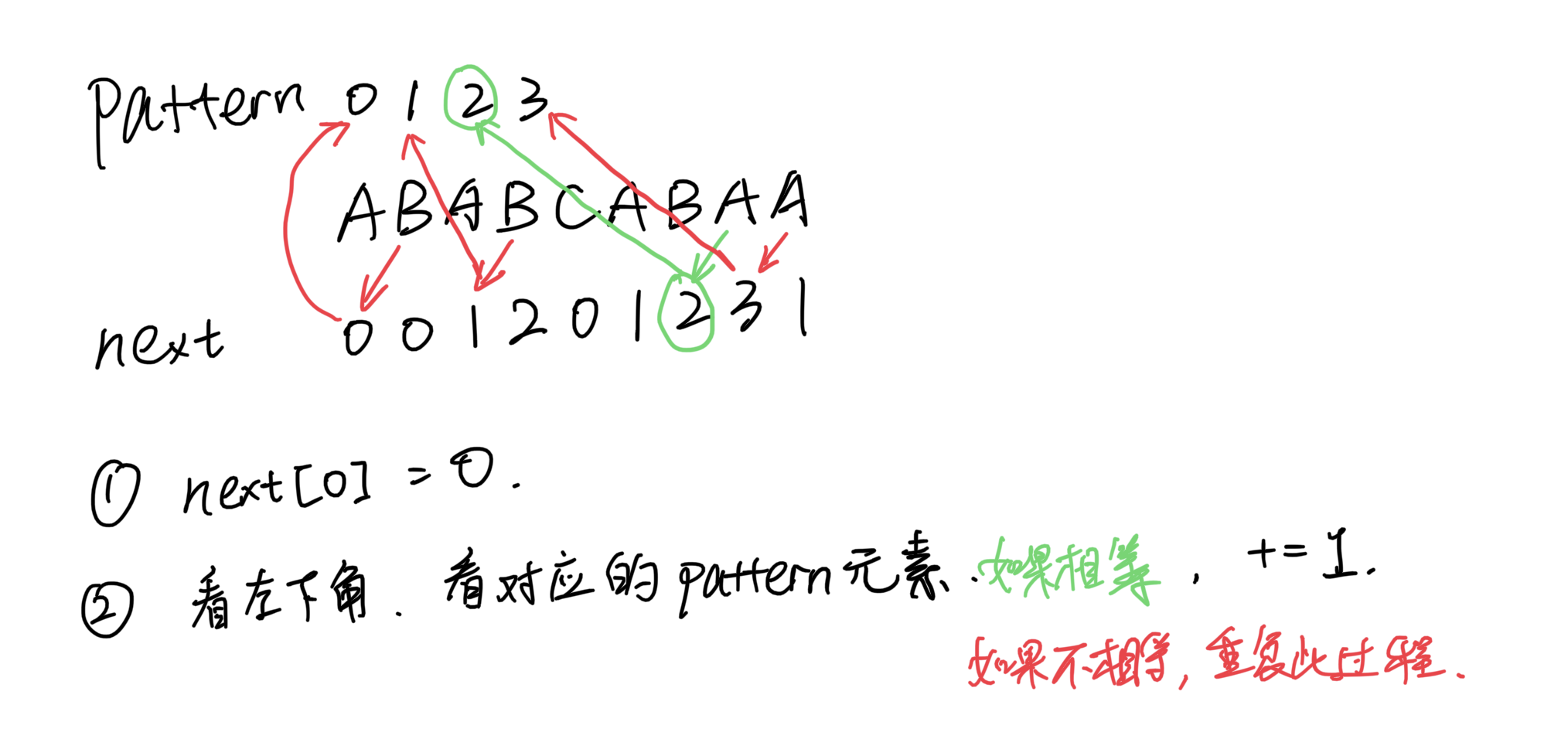
为什么要看左下角对应的pattern元素:

为什么匹配失败时重复此过程是对的(这部分最难理解)
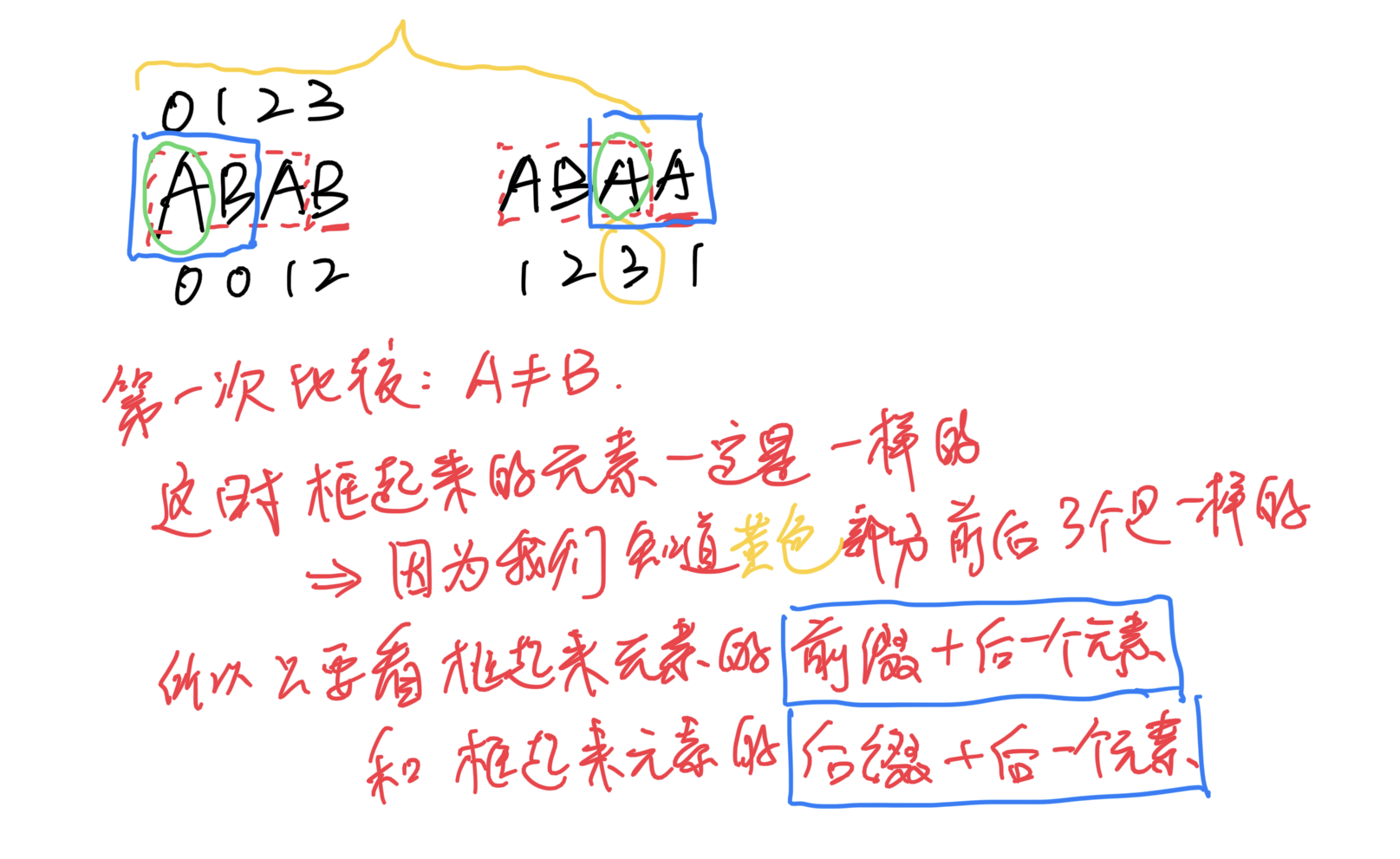
代码实现:
next = [0] * len(pattern)
for i in range(1, len(pattern)):
j = next[i-1]
while j >= 0:
if pattern[j] == pattern[i]:
next[i] = j + 1
break
elif j >= 1:
j = next[j-1]
else:
next[i] = 0
break
等价写法:
next = [0] * len(pattern)
for i in range(1, len(pattern)):
j = next[i-1]
while j >= 1 and pattern[j] != pattern[i]:
j = next[j-1]
if pattern[j] == pattern[i]:
next[i] = j + 1
else:
next[i] = 0
ref: 灯神
28. 实现 strStr()
有了之前的铺垫,应该很简单了。
def strStr(self, haystack: str, needle: str) -> int:
if not needle:
return 0
next = [0] * len(needle)
for i in range(1, len(needle)):
j = next[i-1]
while j >= 1 and needle[j] != needle[i]:
j = next[j-1]
if needle[j] == needle[i]:
next[i] = j + 1
else:
next[i] = 0
j = 0
for i in range(len(haystack)):
while j > 0 and haystack[i] != needle[j]:
j = next[j-1]
if haystack[i] == needle[j]:
if j == len(needle) - 1:
return i - len(needle) + 1
j += 1
return -1
459. 重复的子字符串
两种可能的解法:
一种头尾各移除一个字符,看原串是否是后面字符串的字串;正确性利用同余证明。
另一种用KMP,但是缺乏证明。
KMP时间复杂度
总结
字符串总的来说可以用数组的优化方法,双指针滑动窗口等等。它们常常被包装成”单词问题“”空格问题“等等字符串的场景来做。
字符串另外一个场景就是string matching。之前学61b的时候掌握了rabin-karp算法,现在多了一个KMP算法。