数组第四课,矩阵。
59. 螺旋矩阵 II
这题没什么算法,就是模拟过程。我的解法是一小格一小格来,碰到边就按照“右-下-左-上”的优先级来走。特例是在往上走的时候可能会提早走到右边去,加一个特殊判断即可。
def generateMatrix(self, n: int) -> List[List[int]]:
total = n * n
coord = [0, 0]
res = [[0] * n for _ in range(n)]
goingUp = False
for i in range(1, total + 1):
row = coord[0]
col = coord[1]
res[row][col] = i
if col + 1 < n and res[row][col+1] == 0 and not goingUp: # not hit right
coord[1] += 1
elif row + 1 < n and res[row+1][col] == 0: # not hit bottom
coord[0] += 1
elif col - 1 >= 0 and res[row][col-1] == 0:
coord[1] -= 1
elif row - 1 >= 0 and res[row-1][col] == 0:
goingUp = True
coord[0] -= 1
if not (row - 2 >= 0 and res[row-2][col] == 0):
goingUp = False
else:
break
return res
但是题解的解法更高明一些,它是以边为单位做的,每次循环都是一个子矩形,有效减少了判断频率和复杂度。
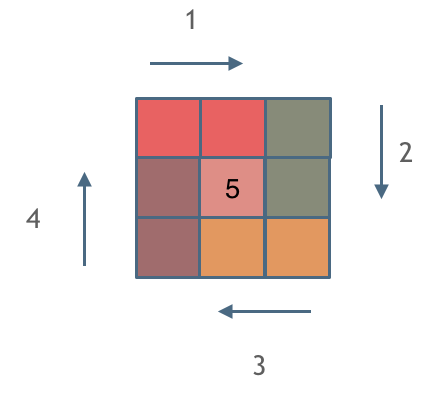
def generateMatrix(self, n: int) -> List[List[int]]:
# 初始化要填充的正方形
matrix = [[0] * n for _ in range(n)]
left, right, up, down = 0, n - 1, 0, n - 1
number = 1 # 要填充的数字
while left < right and up < down:
# 从左到右填充上边
for x in range(left, right):
matrix[up][x] = number
number += 1
# 从上到下填充右边
for y in range(up, down):
matrix[y][right] = number
number += 1
# 从右到左填充下边
for x in range(right, left, -1):
matrix[down][x] = number
number += 1
# 从下到上填充左边
for y in range(down, up, -1):
matrix[y][left] = number
number += 1
# 缩小要填充的范围
left += 1
right -= 1
up += 1
down -= 1
# 如果阶数为奇数,额外填充一次中心
if n % 2:
matrix[n // 2][n // 2] = number
return matrix
54. 螺旋矩阵
相比于上一题,要多考虑只有一行或一列的情况。
def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
res = []
m, n = len(matrix), len(matrix[0])
left, right, up, down = 0, n-1, 0, m-1
while left <= right and up <= down:
for x in range(left, right):
res.append(matrix[up][x])
for y in range(up, down):
res.append(matrix[y][right])
for x in range(right, left, -1):
res.append(matrix[down][x])
if up == down:
break
for y in range(down, up, -1):
res.append(matrix[y][left])
if left == right:
break
left += 1
right -= 1
up += 1
down -= 1
if m == n and m % 2:
res.append(matrix[m//2][n//2])
return res